Set (abstract data type)
In computer science, a set is an abstract data structure that can store certain values, without any particular order, and no repeated values. It is a computer implementation of the mathematical concept of a finite set. Unlike most other collection types, rather than retrieving a specific element from a set, one typically tests a value for membership in a set.
Some set data structures are designed for static or frozen sets that do not change after they are constructed. Static sets allow only query operations on their elements — such as checking whether a given value is in the set, or enumerating the values in some arbitrary order. Other variants, called dynamic or mutable sets, allow also the insertion and/or deletion of elements from the set.
A set can be implemented in many ways. For example, one can use a list, ignoring the order of the elements and taking care to avoid repeated values. Sets are often implemented using various flavors of trees, tries, or hash tables.
A set can be seen, and implemented, as a (partial) associative array, in which the value of each key-value pair has the unit type.
In type theory, sets are generally identified with their indicator function: accordingly, a set of values of type  may be denoted by
may be denoted by 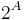 or
or 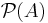 . (Subtypes and subsets may be modeled by refinement types, and quotient sets may be replaced by setoids.) The characteristic function F of a set S is defined as:
. (Subtypes and subsets may be modeled by refinement types, and quotient sets may be replaced by setoids.) The characteristic function F of a set S is defined as: 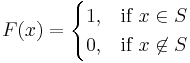
In theory, many other abstract data structures can be viewed as set structures with additional operations and/or additional axioms imposed on the standard operations. For example, an abstract heap can be viewed as a set structure with a min(S) operation that returns the element of smallest value.
Contents |
Operations
Core set-theoretical operations
One may define the operations of the algebra of sets:
union(S,T): returns the union of sets S and T.intersection(S,T): returns the intersection of sets S and T.difference(S,T): returns the difference of sets S and T.subset(S,T): a predicate that tests whether the set S is a subset of set T.
Static sets
Typical operations that may be provided by a static set structure S are:
is_element_of(x,S): checks whether the value x is in the set S.is_empty(S): checks whether the set S is empty.size(S)orcardinality(S): returns the number of elements in S.iterate(S): returns a function that returns one more value of S at each call, in some arbitrary order.enumerate(S): returns a list containing the elements of S in some arbitrary order.build(x1,x2,…,xn,): creates a set structure with values x1,x2,…,xn.create_from(collection): creates a new set structure containing all the elements of the given collection or all the elements returned by the given iterator.
Dynamic sets
Dynamic set structures typically add:
create(): creates a new, initially empty set structure.create_with_capacity(n): creates a new set structure, initially empty but capable of holding up to n elements.
add(S,x): adds the element x to S, if it is not present already.remove(S, x): removes the element x from S, if it is present.capacity(S): returns the maximum number of values that S can hold.
Some set structures may allow only some of these operations. The cost of each operation will depend on the implementation, and possibly also on the particular values stored in the set, and the order in which they are inserted.
Additional operations
There are many other operations that can (in principle) be defined in terms of the above, such as:
pop(S): returns an arbitrary element of S, deleting it from S.map(F,S): returns the set of distinct values resulting from applying function F to each element of S.filter(P,S): returns the subset containing all elements of S that satisfy a given predicate P.fold(A0,F,S): returns the value A|S| after applyingAi+1 := F(Ai, e)for each element e of S.clear(S): delete all elements of S.equal(S1, S2): checks whether the two given sets are equal (i.e. contain all and only the same elements).hash(S): returns a hash value for the static set S such that ifequal(S1, S2)thenhash(S1) = hash(S2)
Other operations can be defined for sets with elements of a special type:
sum(S): returns the sum of all elements of S for some definition of "sum". For example, over integers or reals, it may be defined asfold(0, add, S).nearest(S,x): returns the element of S that is closest in value to x (by some metric).
Implementations
Sets can be implemented using various data structures, which provide different time and space trade-offs for various operations. Some implementations are designed to improve the efficiency of very specialized operations, such as nearest or union. Implementations described as "general use" typically strive to optimize the element_of, add, and delete operations.
Sets are commonly implemented in the same way as associative arrays, namely, a self-balancing binary search tree for sorted sets (which has O(log n) for most operations), or a hash table for unsorted sets (which has O(1) average-case, but O(n) worst-case, for most operations). A sorted linear hash table[1] may be used to provide deterministically ordered sets.
Other popular methods include arrays. In particular a subset of the integers 1..n can be implemented efficiently as an n-bit bit array, which also support very efficient union and intersection operations. A Bloom map implements a set probabilistically, using a very compact representation but risking a small chance of false positives on queries.
The Boolean set operations can be implemented in terms of more elementary operations (pop, clear, and add), but specialized algorithms may yield lower asymptotic time bounds. If sets are implemented as sorted lists, for example, the naive algorithm for union(S,T) will take code proportional to the length m of S times the length n of T; whereas a variant of the list merging algorithm will do the job in time proportional to m+n. Moreover, there are specialized set data structures (such as the union-find data structure) that are optimized for one or more of these operations, at the expense of others.
Language support
One of the earliest languages to support sets was Pascal; many languages now include it, whether in the core language or in a standard library.
- Java offers the
Setinterface to support sets (with theHashSetclass implementing it using a hash table), and theSortedSetsub-interface to support sorted sets (with theTreeSetclass implementing it using a binary search tree). - Apple's Foundation framework (part of Cocoa) provides the Objective-C classes
NSSet,NSMutableSet,NSCountedSet,NSOrderedSet, andNSMutableOrderedSet. The CoreFoundation APIs provide the CFSet and CFMutableSet types for use in C. - Python has built-in
setandfrozensettypes since 2.4, and since Python 3.0 and 2.7, supports non-empty set literals using a curly-bracket syntax, e.g.:{ x, y, z }. - The .NET Framework provides the generic
HashSetandSortedSetclasses that implement the genericISetinterface. - Ruby's standard library includes a
setmodule which containsSetandSortedSetclasses that implement sets using hash tables, the latter allowing iteration in sorted order. - OCaml's standard library contains a
Setmodule, which implements a functional set data structure using binary search trees. - The GHC implementation of Haskell provides a
Data.Setmodule, which implements a functional set data structure using binary search trees. - The Tcl Tcllib package provides a set module which implements a set data structure based upon TCL lists.
As noted in the previous section, in languages which do not directly support sets but do support associative arrays, sets can be emulated using associative arrays, by using the elements as keys, and using a dummy value as the values, which are ignored.
In C++
In C++, the Standard Template Library (STL) provides the set template class, which implements a sorted set using a binary search tree; SGI's STL also provides the hash_set template class, which implements a set using a hash table.
In sets, the elements themselves are the keys, in contrast to sequenced containers, where elements are accessed using their (relative or absolute) position. Set elements must have a strict weak ordering.
Some of the member functions in C++ and their description is given in the table below:
| Signature(s) | Description |
|---|---|
iterator begin(); |
Returns an iterator to the first element of the set. |
iterator end(); |
Returns an iterator just before the end of the set. |
bool empty() const; |
Checks if the set container is empty (i.e. has a size of 0) |
iterator find(const key_type &x) const; |
Searches the container for an element x and if found, returns an iterator to it, or else returns an iterator to set::end |
void insert ( Input Iterator first, Input Iterator last );
|
Inserts an element into the set. The first version returns pair, with its member pair::first set to an iterator pointing to either the newly inserted element or to the element that already had its same value in the set. The pair::second element in the pair is set to true if a new element was inserted or false if an element with the same value existed. And the second version returns an iterator either pointing to newly inserted element or to element having same value in set. |
void clear(); |
Removes all elements in the set, making its size 0. |
Template parameters
Here value_type and iterator are member types defined in set containers. Firstly, value to be used to initialize inserted element. Then position of first element compared for the operation.It actually does not give the position where element is to be inserted but just an indication of possible insertion position in the container so as to make efficient insertion operation. Template type can be any type of input iterator. Iterators specify a range of elements and copies of these in range [first, last) are inserted in set.
Multiset
A variation of the set is the multiset or bag, which is the same as a set data structure, but allows repeated ("equal") values. It is possible for objects in computer science to be considered "equal" under some equivalence relation but still distinct under another relation. Some types of multiset implementations will store distinct equal objects as separate items in the data structure; while others will collapse it down to one version (the first one encountered) and keep a positive integer count of the multiplicity of the element.
- C++'s Standard Template Library provides the
multisetclass for the sorted multiset, and SGI's STL provides thehash_multisetclass, which implements a multiset using a hash table. - For Java, third-party libraries provide multiset functionality:
- Apache Commons Collections provides the
BagandSortedBaginterfaces, with implementing classes likeHashBagandTreeBag. - Google Collections provides the
Multisetinterface, with implementing classes likeHashMultisetandTreeMultiset.
- Apache Commons Collections provides the
- Apple provides the
NSCountedSetclass as part of Cocoa, and theCFBagandCFMutableBagtypes as part of CoreFoundation. - Python's standard library includes
collections.Counter, which is similar to a multiset.
Where a multiset data structure is not available, a workaround is to use a regular set, but override the equality predicate of its items to always return "not equal" on distinct objects (however, such will still not be able to store multiple occurrences of the same object) or use an associative array mapping the values to their integer multiplicities (this will not be able to distinguish between equal elements at all).
See also
References
- ^ Wang, Thomas (1997), Sorted Linear Hash Table, http://www.concentric.net/~Ttwang/tech/sorthash.htm
|
|||||||||||||||||||||||
|
|||||||||||||||||||||||